ADsP 3과목 기초 - 편차와 분산

 

분산

 

· 분산: 데이터들이 중심에서 얼마나 떨어져 있는지를 알아보기 위한 측도다. 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 구한다. 즉, 차이값의 제곱의 평균이다.

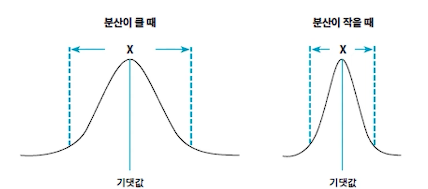
· 확률변수의 분산: 확률변수가 취할 수 있는 값들이 그 중심(모평균)에서 얼마나 떨어져 있는지를 측정하는 측도다. 값이 크면 클수록 확률 X값이 기댓값에서 멀리 떨어져 있을 수 있다.

 

· 표준편차 = √분산 -> 편차에 포함된 음수의 개념을 루트를 씌워서 양의 개념으로 바꾼 값.  

 

+ 확률변수의 분산은 확률변수의 평균과 마찬가지로 이미 측정되어 있는 값에 대한 것이 아니고 앞으로 측정 또는 관측될 가능성이 있는 값들에 대한 측도다.

 

++ 편차는 차이의 개념

+++ 분산은 거리의 개념 따라서 분산은 음의 개념이 올 수 없다. =  퍼짐의 정도 -> 데이터 값에 초점을 맞추는 것이 아니라, 집단 중심의 개념

        ( 그러므로 제곱을 값에 제곱을 함)

 

 

 

 

 

 

 

분산분석 개요  중요 **

 

· 분산분석은 세 개 이상의 모집단이 있을 겅우에 여러 집단 사이의 평균을 비교하는 검정 방법이다.

· 분산분석의 귀무가설은 항상 'Ho : 모든 집단 간 평균은 같다.'이다.

· 분산분석을 수행하기 위해서는 아래의 세 가지 가정사항을 필요로 한다.

1. 정규성: 각 집단의 표본들은 정규분포를 따라야 한다.
2. 등분산성: 각 집단은 동일한 분산을 가져야 한다.
3. 독립성: 각 집단은 서로에게 영향을 주지 않는다.

· 분산분석의 한 가지 단점이 있다면 귀무가설을 기각할 경우 어느 집단 간 평균이 같은지, 혹은 어느
집단 간의 평균이 얼마나 다른지 알 수 없다는 점이다.

· 그래서 분산분석의 귀무가설을 기각했을 경우 어느 집단 간에 차이를 보이는지 알기 위한 사후검정
방법으로 Scheffe, Tukey, Duncan, Fisher's ISD, Dunnett, Bonferroni 등의 방법을 사용한다.

· 분산분석의 독립변수는 범주형 데이터여야 하고, 종속변수는 연속형이어야 한다.

· 분산분석에는 '(집단 간 분산)÷(집단 내 분산)'으로 계산되는 F-value가 사용된다.

· 평균을 비교하는 분산분석에 '분산'의 개념을 사용하는 이유는 집단 간 평균의 분산이 클수록 각 집단
의 평균은 서로 멀리 떨어져 있기 때문이다. 그래서 집단 간 차이를 비교하기 쉬워진다.